Test d'hypothèses
| · | Echantillonage |
| · | Distributions théoriques |
| · | Notions préliminaires |
| · | Test sur la moyenne |
| · | Test de différence de moyennes |
| · | Test sur la variance |
| · | Test sur le rapport de variances |
Distributions
|
|
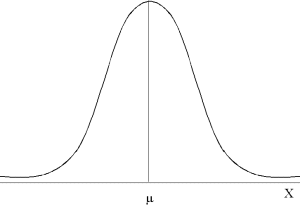
· La distribution normale
La distribution normale ou de Gauss est une curve qui représente une distribution de probabilités. Elle présente les caractéristiques suivantes:
- la distribution est symétrique
- la moyenne, la mode et la mediane sont idéntiques
- le 64% des observations est à l'intérieur de l'intervale m ± s où m et s représentent la moyenne et l'écart-type de la variable
Elle est appélée normale parce qu'elle représente la plupart des variables (par exemple, la taille, le poids des hommes d'une population).
Elle serve comme base de comparation, pour mésurer, par exemple, le degré de symétrie et la kurtosis (le degré d'applatissement).
|
- L'équation de la courbe normale
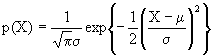
Le calcul de la probabilité à l'aide de cette formule est un peu penible, car il faut appliquer le formule chaque fois qu'on calcule la probabilité d'une variable. L'utilisation de la distribution normale standardisée facilite le travail.
- La distribution normale standardisée
L'idée est de transformer n'importe quelle variable normale à une normale standard avec la transformation suivante.
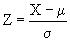
où Z est une transformation linéaire de X, qui a une moyenne "0" et une variance unitaire. Le calcul des probabilités est facilement obtenu à l'aide d'une table normale qu'on trouve dans presque tous les manuels de statistique.
- La courbe normale stardandisée
L'image ci-dessous montre la distribution normale standardisée. La region à droite de la courbe represente la probabilité P(Z > 1.96) = 0.025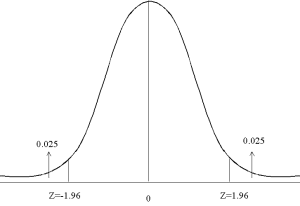
· La distribution c2
La distribution c2 est une distribution asymétrique qui prenne seulement des valeurs positifs. Elle est le résultat d'une somme des carrés de variables normales standardisées indépendantes. Elle a une moyenne égale au nombre de degés de liberté, n, et converge vers une loi normale quand augmente le nombre d'observations.
L'image ci-dessous montre la distribution de la statistique avec n = 10%. La region à droite de la courbe represente la probabilité P(c2> 15.99) = 0.10
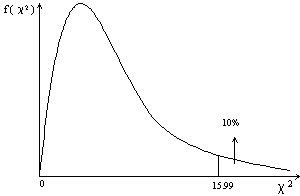
|
· La distribution t-Student
La distribution t-Student est une distribution symétrique qui converge vers la distribution normale quand le nombre d'observations augmente (Quand la taille de l'échantillon est supérieure à 30 on utilise souvent la loi normale). Cette distribution a une moyenne égale à zèro, est biaisée à droite (skewness) et est plus applatit (kurtosis) que la distribution normale. Le nombre de degrés de liberté est égal au nombre de variables indépendants.
L'image ci-dessous montre la distribution de la statistique t avec 10 degrées de liberté. La region à droite de la courbe represente la probabilité P(t > 1.812) = 0.05, et la region à gauche de la courbe represente la probabilité P(t < -1.812) = 0.05
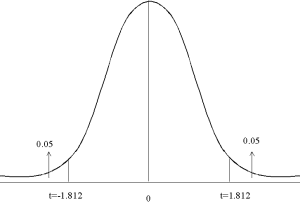
|
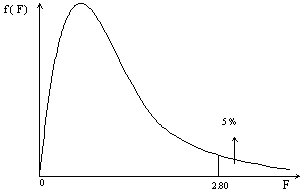
· La distribution F
La distribution F est une distribution asymétrique qui prenne seulement des valeurs positifs. Elle est le résultat du rapport de deux variables c2 indépendantes divisées par les respectifs degrés de liberté.
- La statistique
Si n1 et n2 representent les degrés de liberté de deux variables indépendantes, c21 et c22, la statistique F a une distribution F avec n1 et n2 degrés de liberté.
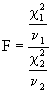
- La courbe
La courbe ci-dessous montre la distribution de la statistique F avec n1 = 9 et n2 = 12 degrés de liberté. La region à droite de la courbe represente la probabilité P(F > 15.99) = 0.05