Rappel de quelques définitions importantes pour définir les algorithmes de recherche

• Complétude
  • Un algorithme de recherche est complet s’il trouve une solution s’il en existe une
• Optimalité
  • Un algorithme de recherche est optimal s’il trouve un chemin optimal (minimal ou maximal) à chaque fois qu’une solution existe
• Complexité
  • La complexité est une estimation du temps et de la quantité de mémoire nécessaire à l’exécution d’un algorithme
• Stratégies aveugles
  • Elles n’exploitent pas les descriptions d’états pour ordonner la file d’attente. Elles n’exploitent que les positions des noeuds dans les arbes de recherche
• Stratégies heuristiques
  • Elles exploitent les descriptions d’états pour ordonner la file d’attente (les noeuds “les plus prometteurs” seront placés au début de la file).

Recherche en largeur

Une recherche en largeur est une recherche de type aveugle. Elle développe noeud le moins profond.

• Complète
• Optimale si le coût d'une étape est unitaire
• Nombre de noeuds produits: 1 + b + b2 + … + bd = (bd+11)/(b1)= O(bd)
• Complexité en temps et en espace est O(bd)

Attention, si un problème n’a pas de solution, la recherche en largeur peut durer indéfiniment (si le nombre d’états est infini ou si les états peuvent être visité un nombre indéfini de fois) => il faut éliminer les boucles.


Pour voir comment fonctionne cette recherche, prenez connaissance de l'animation ci-dessous.

Recherche en profondeur

Une recherche en pronfondeur est une recherche de type aveugle. Elle développe noeud le plus profond.

• Complète seulement si l'arbre est fini
• Non optimale
• Nombre de noeuds produits (dans le pire des cas): 1 + b + b2 + … + bm = O(bm)
• Complexité en temps O(bm)
• Complexité en espace O(bm) [ou O(m)]

Pour voir comment fonctionne cette recherche, prenez connaissance de l'animation ci-dessous.

Algorithme MinMax

Cet algorithme est un algorithme de jeux, ce qui comporte un joueur et un adversaire. Nous avons donc un agent (MIN) qui est en compétition avec notre agent (MAX). Min veut que Max échoue, et inversement. Un gain pour max est une perte pour Min, et inversément.
Aucun plan peut garantir le succès de MAX quelles que soient les actions que MIN réalise, mais ceci est vrai pour Min. À chaque tour, le choix de l'action à réaliser doit être fait dans une limite de temps spécifiée. L'espace d'états est très grand: seule une petite fraction de cet espace peut être explorée dans le temps limité imparti.

• La présence d'un adversaire introduit un élément d'incertitude. Tous les mouvements ne sont pas contrôllés par l'ordinateur.
• Les programmes de jeu doivent savoir faire face aux imprévus
• Les jeux intéressants sont trop complexes pour envisager une solution exhaustive. Par exemple les échecs on un facteur de branchement d'environ 35! .
• Le but à chaque pas est de choisir le prochain meilleur coup à jouer.
• Les coûts doivent être évalués d'une manière optimale.
• Une fonction heuristique permet d'estimer s'il y a gain, perte ou match nul

Marche à suivre pour l'algorithme Min et Max:

1. Etendre l'arbre de jeu uniformément de l'état courant (où c'est à MAX de jouer) jusqu'à une profondeur h.
2. Calculer la fonction d'évaluation pour chacun des noeuds terminaux de l'arbre.
3. Remonter les valeurs des feuilles vers la racine de l'arbre de sorte que:
   • Un noeud MAX reçoive la valeur maximum des évaluations de ses successeurs.
   • Un noeud MIN reçoive la valeur minimum des évaluations de ses successeurs.
4. Sélectionner le coup menant à un noeud MIN ayant la valeur remontée la plus grande.

Stratégie de jeu pour Max:

1. Séléctionner un mouvement en utilisant MinMAx
2. Éxécuter le mouvement de Max
3. Observer le mouvement de Min

Propriétés de Min et Max

• Complet si l'arbre de jeu est fini
• Optimal si l'adversaire est aussi optimal
• Complexité en temps: O(bh) où b est le facteur de branchement et h est l'horizon de recherche
• Complexité en place: O(bh) (exploration en profondeur) pour les échecs: avec b = 35 et h = 100

L'algorithme Min et Max peut être simplifiée grâce à l'agorithme d'élagage α - β
Principe de l'élagage:

1. étendre l'arbre de jeu jusqu'à une profondeur h par recherche en profondeur
2. Ne plus générer les successeurs d'un noeud dès qu'il est évident que ce noeud ne sera pas choisi (compte tenu des noeuds déjà examinés)
   • chaque noeud MAX garde la trace d'une α valeur = valeur de son meilleur successeur trouvé jusqu'ici
   • chaque noeud MIN garde la trace d'une β valeur = valeur de son plus mauvais successeur trouvé jusqu'ici
   • valeurs initiales: α = −∞ et β = +∞

Pour mieux comprendre le comportement de l'algorithme Min et Max ainsi que le principe de l'élagage, regardez la vidéo ci-dessous:

Recherche Aveugle

Notation Grand O

La notation grand O est utilisée pour classifier les agorythmes.
O pour Ordre => la vitesse de croissance d'une fonction.
f(x) = O(g(x)) signifie que f ne croît pas plus vite que g.
Pour résoudre les exercices sans trop de difficulté, garder en tête que:
lim(f(x))=C*lim(O(g(x)))
Souvent dans les exercices on nous demande de trouver C.
On peut le calculer si les deux côtés de l'equation sont à
la même puissance, sinon on met un < ou > et on ignore C.
Ex: 1 < O(n)

Définitions et Concepts

évaluation des méthodes de recherche:

• Complétude: Un algorithme est complet s'il trouve une solution lorsqu'il existe une solution.
• Optimalité: un algorithme est optimal s'il trouve la meilleure solution lorsqu'il en existe plusieurs.
• Complétude probabiliste: si une solution existe, la probabilité que l'algorithme la trouve tend rapidement vers 1 avec la durée de l'execution.
• Complexité en temps: le nombre de noeuds nécessaires pour trouver la solution.
• Complexité en espace: le nombre maximum de noeuds à conserver en mémoire pour trouver la solution.
• b: branchement, le nombre maximum de successeurs pour un état.
• d: profondeur du meilleur noeud solution.
• m: profondeur maximum (peut être infinie)
• File d'attente: Donne l'ordre dans lequel les noeuds seront parcourus. Selon le type de recherche, les noeuds découverts seront insérés en tête ou en queue de la liste.
• Arbres:

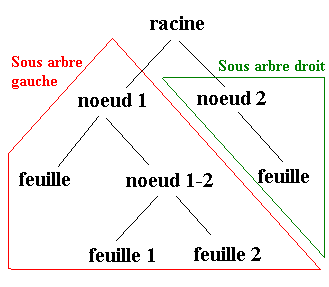
• Noeud: élément d'une structure de données dans un arbre. Peut être infini. Possède les champs:
• état-parent-enfant-profondeur-coût de chemin (g(x))
• État: représentation d'une configuration réelle. Nombre fini.

Les stratégies de recherches aveugles ne regardent pas les descriptions d'état, mais uniquement les positions des noeuds dans l'arbre de recherche, au contraire des stratégies de recherches heuristiques.

Objectif de la stratégie de recherche:

Résoudre chaque instance aussi efficacement que possible.
La racherche aveugle explose systématiquement les alternatives. Les stratégies de recherche aveugle sont:

I) La recherche en largeur

• complète
• optimale si le coût d'une étape est 1


• Développer le noeud le moins profond. Insertion des sucesseurs à la fin de la file d'attente.
• Nombre de noeuds produits = O(b^d) où b est le facteur de branchement et d est la profondeur atteinte lors de la recherche.
• Complexité en temps et en espace = O(b^d)

Problème: s'il n'y a pas de solution, la recherche en largeur peut durer indéfiniment (si c'est un arbre infini ou contenant des boucles).

II) La recherche en profondeur

• non-complète, échoue dans les espaces cycliques ou infinis
• non-optimale


• Développer le noeud le plus profond. Insertion des sucesseurs au début de la file d'attente.
• Nombre de noeuds produits = O(b^m) où b est le facteur de branchement et m est la profondeur maximale d'un noeud feuille.
• Complexité en temps = O(b^m) = terrible si m>>>d
• Complexité en espace = O(b * m) ou O(m) linéaire!
• A besoin de beaucoup moins d'espace que la recherche en largeur.

III) La recherche en profondeur limitée

• complète si L ≥ d
• non-optimale


• Recherche en profondeur avec une limite de profondeur d'exploration L.
• Les noeuds de profondeur L ne sont pas développés.
• Complexité en temps = O(b^L)
• Complexité en espace = O(b * L) ou O(L)

Problème: Il est possible que la solution ne soit pas dans les limites de la recherche.

Solution:

IIIb) Recherche par approfondissement itératif (IDS)

• complète
• optimale


• Répéter la recherche pour L = 1; 2; 3; 4; ...
• Rien n'est stocké en mémoire, l'action est simplement répétée
• Combine les avantages des recherches en largeur et en profondeur.
• économe en espace:
  • Complexité en temps = O(b^d)
  • Complexité en espace = O(d)

IV) La recherche bi-directionnelle

• complète
• optimale


• Recherche en largeur de l'état solution à partir de l'état initial ET recherche en largeur de l'état initial à partir de l'état solution.
• La recherche s'arrête quand les deux processus se renvontrent.
• Complexité en temps et en espace = O(b^d/2) ce qui ens bien plus petit que O(b^d)

tp2.html