La Terre et ses représentations
Pour se déplacer sur la Terre, il faut des repères. Les hommes ont défini deux points : les
pôles, et ont imaginé une sorte de quadrillage de la surface du globe terrestre.
Les lignes horizontales sont les parallèles.
l’équateur, les cercles polaires et les parallèles permettent de mesurer la
latitude en degré, c’est-à-dire l’éloignement d’un lieu par rapport à
l’équateur. On peut ainsi s’écarter de l’équateur en allant vers le nord (latitude N), ou vers le sud (latitude S).
Les lignes verticales sont les méridiens.
Les méridiens permettent de mesurer la longitude en degré, c’est-à-dire l’éloignement d’un lieu par rapport au méridien d’origine (méridien de
Greenwich). On peut ainsi s’écarter du méridien d’origine en allant vers l’ouest (longitude O ou W), ou vers l’est (longitude E).
Le globe est la représentation la plus exacte et la plus fidèle de la Terre. Le globe montre la répartition des terres, des océans et des mers qui se distinguent par leur couleur.
Pour des raisons pratiques les géographes utilisent des représentations à plat de la sphère terrestre. Mais il est impossible de représenter sans déformation les caractéristiques de la Terre, qui est une boule, sur une feuille qui est une surface plane.
Les déformations ne sont pas les mêmes suivant le système de projection utilisé.
Qu'est-ce qu'une projection cartographique?
On appelle projection cartographique le système de correspondance entre les coordonnées géographiques et les points du plan de projection. On fait appel à la géométrie et plus couramment aux formules mathématiques pour réaliser ce système de projection.
En termes de géométrie, la Terre, en tant qu'ellipsoïde (une sphère légèrement aplatie), est considérée comme une forme non-développable.
En effet, peu importe la manière dont la Terre est divisée, elle ne peut être déroulée ou dépliée pour être étendue. Certaines des projections les plus simples se définissent d'après des propriétés géométriques générales que l'on peut étendre sans déchirer leurs surfaces. On considère ces figures développables.
Les cônes, les cylindres et les «plans» sont des exemples de figures qui reflètent ces propriétés.
Ainsi comme vous pouvez le constater sur la représentation en 3D ci-dessous, la surface courbe de la Terre peut être projetée sur les formes qui peuvent être déroulées pour devenir une carte plate.
Les différentes projections
Projection de Mercator
C'est une projection cylindrique directe.
Le cylindre est tangent ou sécant à l'équateur.
Les méridiens sont représentés par des droites parallèles équidistantes.
Les parallèles sont représentés par des droites orthogonales aux méridiens.
Projection de Lambert
C'est une projection conique.
Le cône est tangent ou sécant à un parallèle que l'on appelle le parallèle origine ou isomètre central (de lattitude j)
Les méridiens sont représentés par des droites concourantes au pôle.
Les parallèles sont représentés par des cercles concentriques au pôle.
Projection Stéréographique Polaire
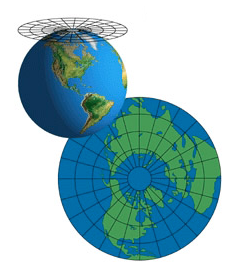C'est une projection azimutale conforme.
Le plan est tangent (ou sécant) à un pôle.
Les méridiens sont représentés par des droites concourantes au pôle.
Les parallèles sont des cercles concentriques au pôle.
Les caractéristiques recherchées dans les projections
Elles sont les suivantes :
• conservation des surfaces (projection équivalente) ;
• conservation des angles (projection est conforme) ;
• conservation des distances (le long de grands cercles) ;
• représentation des grands cercles par des droites (projection orthodromique).
Choisir une projection c’est faire un compromis sur les propriétés recherchées.
Ressources
"
Page créée par Fatima Chokri le 30 Avril 2016.
Dernière mise à jour le 4 Mai 2016.
Validated HTML with W3C